Question

You wish to buy a cabin in 15 years. TODAY, the cabin costs $150,000. You believe the price of the cabin will inflate at 4% annually. You want to invest a single amount of money (lump sum) today and have the money grow to equal the future purchase price of the cabin 15 years from now. If you can earn 10% annually on your investments, how much do you need to invest NOW, in order to be able to purchase the cabin?

Answer 1

I will need to invest 64,669.73 dollars now.

Step-by-step explanation:

We will calcualte the future value of the cabin considering the inflation:

`Principal \: (1+ inflation )^(time) = Amount`

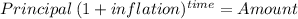
Principal 150,000.00

time 15 years

inflation 0.04000

`150000 \: (1+ 0.04)^(15) = Amount`

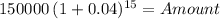
Amount 270,141.53

Then we calculate the present value of the lump sum at 15 years discounted at 10% which is the yield of the funds

`(Maturity)/((1 + rate)^(time) ) = PV`

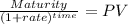
Maturity 270,141.53

time 15 years

rate 0.10

`(270141.53)/((1 + 0.1)^(15) ) = PV`

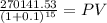
PV 64,669.73

we would need to deposit 64,669.73 today to get enough cash to purchase the bcabin in 15 years.