Answer:
B. 4,200±CONFIDENCE.T(0.10,140,12)
Explanation:
We are in posession's of the sample standard deviation, so the t-distribution is used.
The confidence interval is a function of the sample mean and the margin of error.
That is:
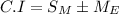
In which
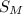 is the sample mean, and the
is the sample mean, and the
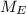 is the margin of error, related to the confidence level, the sample's standard deviation and the sample size.
is the margin of error, related to the confidence level, the sample's standard deviation and the sample size.
So the correct answer is:
B. 4,200±CONFIDENCE.T(0.10,140,12)