Question

Mariah started to find the solutions of x2 + 4x + 1 = 0. Her work is shown below. x2 + 4x + 1 = 0 x2 + 4x = –1 x2 + 4x + 4 = –1 + 4 (x + 2)2 = 3 Which describes the solutions of the equation?

since -2 and 3 are both rational, the sum and difference are both rational
since -2 and /3 are both rational, the sum and difference are both rational
since -2 is rational and /3 is irrational, the sum and difference are irrational.
Since /2 is rational and /3 is irrational, the sum and difference are irrational.

Answer 1

C

Since –2 is rational and StartRoot 3 EndRoot is irrational, the sum and difference are irrational.

Explanation:

Answer 2

Since -2 is rational and √3 is irrational, the sum and difference are irrational.

Explanation:

Given equation,

`x^2 + 4x + 1 =0`

`x^2 + 4x = -1`

`x^2 + 4x + 4 = -1+4`

`(x+2)^2 = 3`

`x+2=\pm √(3)`

`x=-2\pm √(3)`

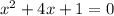
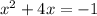
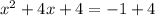
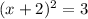
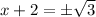
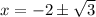
Which is the solution of given equation.

Now, an integer is always a rational number ( that can be expressed as
`(p)/(q)`, where, p and q are integers such that q ≠ 0 ),

So, -2 is a rational number,

Now, √3 can not be expressed as p/q so it is an irrational number,

We know that sum and difference of rational and irrational number is always irrational.

Thus, -2 + √3 and -2 - √3 are irrational.