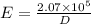Answer:
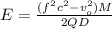
Part c)
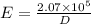
Step-by-step explanation:
Part a)
As per Coulomb's law we know that force on a charge placed in electrostatic field is given as
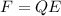
now acceleration of charge is given as
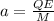
now if charge moved through the distance D in electric field and its speed changes from vo to fraction f of speed of light c
then we will have
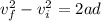
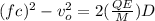
so we have
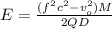
Part b)
Now using work energy theorem we can say that total work done by electric force on moving charge will convert into kinetic energy
So we will have
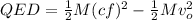
so we have

Part c)
Now if an electron is accelerated using this field
then we have
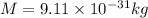
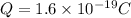
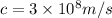
so we have