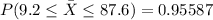Question

Suppose a simple random sample of size nequals=6464 is obtained from a population with mu equals 84μ=84 and sigma equals 16σ=16. ​(a) Describe the sampling distribution of x overbarx. ​(b) What is Upper P (x overbar greater than 87.6 )P x>87.6​? ​(c) What is Upper P (x overbar less than or equals 79.2 )P x≤79.2​? ​(d) What is Upper P (81.3 less than x overbar less than 87.6 )P 81.3

Answer 1

a.
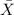`\bar X` is distributed
`N(84;4)`

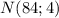
b.
`P(\bar X \geq 87.6) = 0.03593`

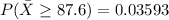
c.
`P(\bar X \leq 79.2) = 0.00820`

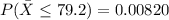
d.
`P(\79.2 \leq \bar X \leq 87.6) = 0.95587`

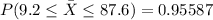
Explanation:

a.

The central limit theorem states that, for large n, the sampling distribution of the sample mean is approximately normal with mean
`\µ` and variance
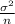`(\sigma^2)/(n)`, then, the sample mean is distributed as a normal random variable with means
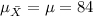`\mu_(\bar X)=\mu=84` and variance
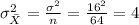`\sigma^2_(\bar X)=(\sigma^2)/(n)=(16^2)/(64)=4`.

b.

`P(\bar X \geq 87.6) = 0.03593`

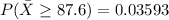
c.

`P(\bar X \leq 79.2) = 0.00820`

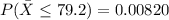
d.

`P(\79.2 \leq \bar X \leq 87.6) = 0.95587`