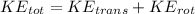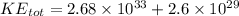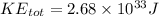Answer:
Part a)
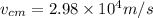
Part b)
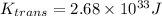
Part c)

Part d)
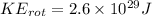
Part e)
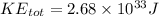
Step-by-step explanation:
Time period of Earth about Sun is 1 Year
so it is

now we know that angular speed of the Earth about Sun is given as
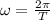
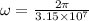
now speed of center of Earth is given as
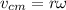
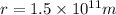
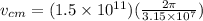
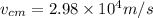
Part b)
now transnational kinetic energy of center of Earth is given as
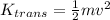
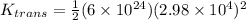
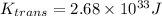
Part c)
Angular speed of Earth about its own axis is given as
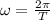
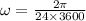

Part d)
Now moment of inertia of Earth about its own axis
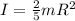

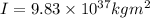
now rotational energy is given as
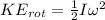

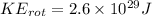
Part e)
Now total kinetic energy is given as