Question

An Article in the Journal of Sports Science (1987, Vol. 5, pp. 261-271) presents the results of an investigation of the hemoglobin level of Canadian Olympic ice hockey players. A random sample of 20 players is selected and the hemoglobin level is measured. The resulting sample mean and standard deviation(g/dl) are and Use this information to calculate a 95% two-sided confidence interval on the mean hemoglobin level and a 95% two-sided confidence interval on the variance. Assume the data are normally distributed. Round your answers to 2 decimal places.

Answer 1

The 95% confidence interval for the population variance is
`\left[0.219, \hspace{0.1cm} 0.807\right]\\\\`

The 95% confidence interval for the population mean is
`\left [15.112, \hspace{0.3cm}15.688\right]`

Explanation:

To solve this problem, a confidence interval of
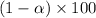`(1-\alpha) * 100%` for the population variance will be calculated.

`$$Sample variance: $S^2=(0.6152)^2$\\Sample size $n=20$\\Confidence level $(1-\alpha)*100\%=95\%$\\$\alpha: \alpha=0.05$\\$\chi^2$ values (for a 95\% confidence and n-1 degree of freedom)\\$\chi^2_{\left (1-(\alpha)/(2);n-1\right )}=\chi^2_((0.975;19))=8.907\\$\chi^2_{\left ((\alpha)/(2);n-1\right )}=\chi^2_((0.025;19))=32.852\\\\`

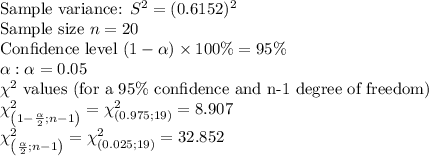
Then, the
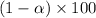`(1-\alpha) * 100%` confidence interval for the population variance is given by:

`\left [\frac{(n-1)S^2}{\chi^2_{\left ((\alpha)/(2);n-1\right )}}, \hspace{0.3cm}\frac{(n-1)S^2}{\chi^2_{\left (1-(\alpha)/(2);n-1\right )}} \right ]\\\\`Thus, the 95% confidence interval for the population variance is:
`\\\\\left [((19-1)(0.6152)^2)/(32.852), \hspace{0.1cm}((19-1)(0.6152)^2)/(8.907) \right ]=\left[0.219, \hspace{0.1cm} 0.807\right]\\\\`

On other hand,

A confidence interval of
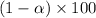`(1-\alpha) * 100%` for the population mean will be calculated

`$$Sample mean: $\bar X=15.40$\\Sample variance: $S^2=(0.6152)^2$\\Sample size $n=20$\\Confidence level $(1-\alpha)*100\%=95\%$\\$\alpha: \alpha=0.05$\\T values (for a 95\% confidence and n-1 degree of freedom) T_((\alpha/2;n-1))=T_((0.025;19))=2.093\\\\$Then, the (1-\alpha) * 100$\% confidence interval for the population mean is given by:\\\\`

\
`\left[ \bar X - T_((\alpha/2;n-1)\sqrt{(\S^2)/(n)}, \hspace{0.3cm}\bar X + T_((\alpha/2;n-1)\sqrt{(\S^2)/(n)} \right ]\\\\`Thus, the 95\% confidence interval for the population mean is:
`\\\\\left [15.40 - 2.093\sqrt{((0.6152)^2)/(19)}, \hspace{0.3cm}15.40 + 2.093\sqrt{((0.6152)^2)/(19)} \right ]=\left [15.112, \hspace{0.3cm}15.688\right] \\\\`