Question

Question Help Suppose that the lifetimes of light bulbs are approximately normally​ distributed, with a mean of 5656 hours and a standard deviation of 3.33.3 hours. With this​ information, answer the following questions. ​(a) What proportion of light bulbs will last more than 6262 ​hours? ​(b) What proportion of light bulbs will last 5252 hours or​ less? ​(c) What proportion of light bulbs will last between 5858 and 6262 ​hours? ​(d) What is the probability that a randomly selected light bulb lasts less than 4646 ​hours? ​(a) The proportion of light bulbs that last more than 6262 hours is

Answer 1

a)3.438% of the light bulbs will last more than 6262 hours.

b)11.31% of the light bulbs will last 5252 hours or less.

c) 23.655% of the light bulbs are going to last between 5858 and 6262 hours.

d) 0.12% of the light bulbs will last 4646 hours or less.

Explanation:

Normally distributed problems can be solved by the z-score formula:

On a normaly distributed set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a value X is given by:

`Z = (X - \mu)/(\sigma)`

After we find the value of Z, we look into the z-score table and find the equivalent p-value of this score. This is the probability that a score will be LOWER than the value of X.

In this problem, we have that:

The lifetimes of light bulbs are approximately normally​ distributed, with a mean of 5656 hours and a standard deviation of 333.3 hours.

So
`\mu = 5656, \sigma = 333.3`

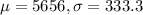
(a) What proportion of light bulbs will last more than 6262 ​hours?

The pvalue of the z-score of
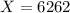`X = 6262` is the proportion of light bulbs that will last less than 6262. Subtracting 100% by this value, we find the proportion of light bulbs that will last more than 6262 hours.

`Z = (X - \mu)/(\sigma)`

`Z = (6262 - 5656)/(333.3)`

`Z = 1.82`

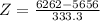
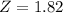
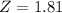`Z = 1.81` has a pvalue of .96562. This means that 96.562% of the light bulbs are going to last less than 6262 hours. So

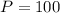`P = 100% - 96.562% = 3.438%` of the light bulbs will last more than 6262 hours.

​(b) What proportion of light bulbs will last 5252 hours or​ less?

This is the pvalue of the zscore of
`X = 5252`

`Z = (X - \mu)/(\sigma)`

`Z = (5252- 5656)/(333.3)`

`Z = -1.21`

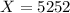
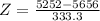
`Z = -1.21` has a pvalue of .1131. This means that 11.31% of the light bulbs will last 5252 hours or less.

(c) What proportion of light bulbs will last between 5858 and 6262 ​hours?

This is the pvalue of the zscore of
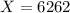`X = 6262` subtracted by the pvalue of the zscore
`X = 5858`

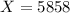
For
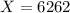`X = 6262`, we have that
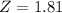`Z = 1.81` with a pvalue of .96562.

For X = 5858

`Z = (X - \mu)/(\sigma)`

`Z = (5858- 5656)/(333.3)`

`Z = 0.61`

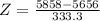
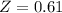
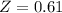`Z = 0.61` has a pvalue of .72907.

So, the proportion of light bulbs that will last between 5858 and 6262 hours is

`P = .96562 - .72907 = .23655`

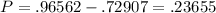
23.655% of the light bulbs are going to last between 5858 and 6262 hours.

​(d) What is the probability that a randomly selected light bulb lasts less than 4646 ​hours?

This is the pvalue of the zscore of
`X = 4646`

`Z = (X - \mu)/(\sigma)`

`Z = (4646- 5656)/(333.3)`

`Z = -3.03`

`Z = -3.03` has a pvalue of .0012. This means that 0.12% of the light bulbs will last 4646 hours or less.