Question

A CBS News/New York Times survey found that 97% of Americans believe that texting while driving should be outlawed (CBS News website, January 5, 2015). a. For a sample of 10 Americans, what is the probability that at least 8 say that they believe texting while driving should be outlawed? Use the binomial distribution probability function to answer this question (to 4 decimals).

Answer 1

Answer: 0.9972

Explanation:

Given : The proportion of Americans believe that texting while driving should be outlawed : p= 0.97

Sample size : n= 10

Using Binomial distribution , the probability of getting success in x trials is given by:-

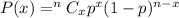`P(x)=^nC_xp^x(1-p)^(n-x)`, where p is probability of success in each trial and n is sample size.

Then, the probability that at least 8 say that they believe texting while driving should be outlawed will be :_

`P(x\geq8)=P(8)+P(9)+P(10)\\\\=^(10)C_(8)(0.97)^8(0.03)^2+^(10)C_(9)(0.97)^9(0.03)^1+^(10)C_(10)(0.97)^(10)(0.03)^0\\\\=(10!)/(8!2!)(0.97)^8(0.03)^2+(10)(0.97)^(9)(0.03)+(0.97)^(10)\ \ \because\ ^nC_(n-1)=n\ \&\ ^nC_(n)=1\\\\=0.997235050549\approx0.9972`

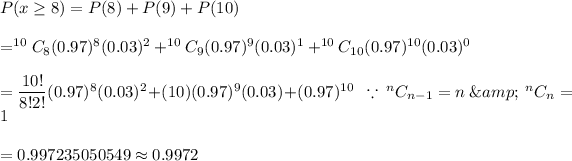
Hence, the required probability = 0.9972