Answer:
The range of possible temperatures is the interval [80.5°,95.5°]
Explanation:
Let
x -----> possible temperatures for that day.
we know that
The absolute value inequality of the difference of the possible temperatures and the temperature at noon must be less than or equal to 7.5° F
so

Solve the absolute-value inequality
First case (positive case)
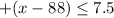
Adds 88 both sides

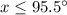
Second case (negative case)

Multiply by -1 both sides
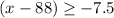
Adds 88 both sides
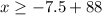
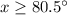
therefore
The range of possible temperatures is the interval [80.5°,95.5°]