Question

Whenever two Apollo astronauts were on the surface of the Moon, a third astronaut orbited the Moon. Assume the orbit to be circular and 270 km above the surface of the Moon, where the acceleration due to gravity is 1.27 m/s2. The radius of the Moon is 1.70 ✕ 106 m. Determine the astronaut's orbital speed.

Answer 1

`v  =  1,582 \ (m)/(s)`

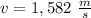
Step-by-step explanation:

We know that for circular motion the centripetal acceleration
`a_c` is:

`a_c = (v^2)/(r)`

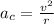
where v is the speed and r is the radius.

The centripetal acceleration for the astronaut must be the gravitational acceleration due to the gravity, as there are no other force. So

`a_c = 1.27 (m)/(s^2)`.

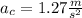The radius of the orbit must be the radius of the Moon, plus the 270 km above the surface

`r = 1.7 * 10^6 \ m + 270  \ km`

`r = 1.7 * 10^6 \ m + 270 * 10^3 \ m`

`r = 1.7 * 10^6 \ m + 0.270 * 10^6 \ m`

`r = 1.97 * 10^6 \ m`

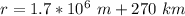
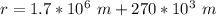
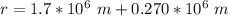
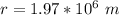
We can obtain the speed as:

`v^2  = a_c r`

`v  = √(a_c r)`

`v  = \sqrt{1.27 (m)/(s^2) * 1.97 * 10^6 \ m}`

`v  = \sqrt{ 2.509 \ 10^6 \ (m^2)/(s^2)}`

`v  =  1.582 \ 10^3 \ (m)/(s)`

`v  =  1,582 \ (m)/(s)`

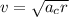
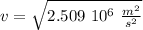
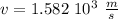
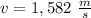
And this is the orbital speed.