Question

The following is the frequency distribution for the speeds of a sample of automobiles traveling on an interstate highway.

Speed (MPH) Frequency
50 − 54 2
55 − 59 4
60 − 64 5
65 − 69 10
70 − 74 9
75 − 79 5

The mean is
(A) 35
(B) 10
(C) 67
(D) 670

Answer 1

The mean is c). 67

Explanation:

You must use the weighted average in order to calculate the mean, given that we know the frequency distribution.

In order to to this, you calculate the proportion that the frequency on each interval represents out of the total frequencies; in other words, this is the weight value:

`2+4+5+10+9+5=35`

`2/35= 0.06\\4/35=0.11\\5/35=0.14\\10/35=0.29\\9/35=0.26\\5/35=0.14`

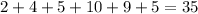
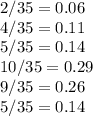
These are the factors by which you will multiply the speed so that you can get the average speed in terms of their weight. For each interval of speed, let's take the average between the minimum and the maximum as the value of speed.

After these two transformations, your table will look as this:

`Speed-Frequency\\52-0.06\\57-0.11\\62-0.14\\67-0.29\\72-0.26\\77-0.14`

Then, you multiply the average speed times its weight value, finding the weighting factor:

`2.97\\6.51\\8.86\\19.14\\18.51\\11.00`

The final step is to sum all the weighting factors, which gives you a total of 67 mph. This is your weighted average.