Question

(a) The plane y + z = 13 intersects the cylinder x2 + y2 = 25 in an ellipse. Find parametric equations for the tangent line to this ellipse at the point (3, 4, 9). (Enter your answer as a comma-separated list of equations. Let x, y, and z be in terms of t.)

Answer 1

Explanation:

We have a curve (an ellipse) written as the system of equations

`\begin{cases} y+z &= 13\\ x^2+y^2 &= 25\end{cases}`.

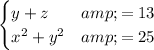And we want to calculate the tangent at the point (3,4,9).

The idea in this problem is to consider two variables as functions of the third. Usually we consider
`y` and
`z` as functions of
`x`. Recall that a curve in the space can be written in parametric form in terms of only one variable. In this case we are considering the ‘‘natural’’ parametrization
`(x, y(x), z(x))`.

Recall that the parametric equation of a line has the form

`r(t)=\begin{cases} x(t) &= x_0 + v_1t \\ y(t) &= y_0 +v_2t\\ z(t) &= z_0 +v_3t \end{cases}`,

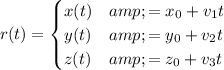where
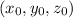`(x_0,y_0,z_0)` is a point on the line (in this particular case is (3,4,9)) and
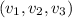`(v_1,v_2,v_3)` is the direction vector of the line. In this case, the direction vector of the line is the tangent vector of the ellipse at the point (3,4,9).

Now, if we have the parametric equation of a curve
`(x, y(x), z(x))` its tangent line will have direction vector
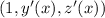`(1, y'(x), z'(x))`. So, as we need to calculate the equation of the tangent line at the point
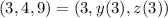`(3,4,9) = (3, y(3), z(3))`, we must obtain the tangent vector
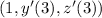`(1, y'(3), z'(3))`. This part can be done taking implicit derivatives in the systems that defines the ellipse.

So, let us write the system as

`\begin{cases} y(x)+z(x) &= 13\\ x^2+y^2(x) &= 25\end{cases}`.

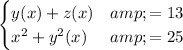Then, taking implicit derivatives:

`\begin{cases} y'(x)+z'(x) &= 0 \\ 2x+2y(x)y'(x) &= 0\end{cases}`.

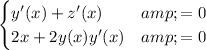Now we substitute the values
`x=3` and
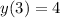`y(3)=4`, and we get the system of linear equations

`\begin{cases} y'(3)+z'(3) &= 0 \\ 2\cdot 3+2\cdot 4y'(x) &= 0\end{cases}`,

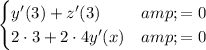where the unknowns are
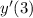`y'(3)` and
`z'(3)`.

The system is

`\begin{cases} y'(3)+z'(3) &= 0 \\ 6+8y'(x) &= 0\end{cases}`,

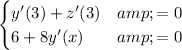and its solutions are

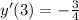`y'(3) = -(3)/(4)` and
`z'(3) = (3)/(4)`.

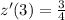Then, the direction vector of the tangent is

`(1, -(3)/(4), -(3)/(4))`.

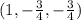Finally, the tangent line has parametric equation

`r(t)=\begin{cases} x(t) &= 3 + t \\ y(t) &= 4 -(3)/(4)t\\ z(t) &= 9 +(3)/(4)t \end{cases}`

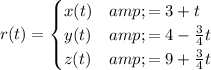
where
`t\in\mathbb{R}`.