Question

A point charge with charge q1 = 4.00 μC is held stationary at the origin. A second point charge with charge q2 = -4.40 μC moves from the point ( 0.155 m , 0) to the point ( 0.245 m , 0.270 m ). How much work W is done by the electric force on the moving point charge?

Answer 1

W=0.94J

Step-by-step explanation:

Electrostatic potential energy is the energy that results from the position of a charge in an electric field. Therefore, the work done to move a charge from point 1 to point 2 will be the change in electrostatic potential energy between point 1 and point 2.

This energy is given by:

`U=(K\left |q_1 \right |\left |q_2 \right |)/(r)\\`

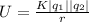
So, the work done to move the chargue is:

`W=U_1-U_2\\W=(K\left |q_1 \right |\left |q_2 \right |)/(r_1)-(K\left |q_1 \right |\left |q_2 \right |)/(r_2)\\r_1=√(((0.155 m)^2+0 m)^2)=0.115m\\r_2=√(((0.245 m)^2+(0.270 m)^2)=0.365m\\W=K\left |q_1 \right |\left |q_2 \right |((1)/(r_1)-(1)/(r_2))\\W=8.99*10^9(Nm^2)/(c^2)(4.00*10^(-6)C)(4.40*10^(-6)C)((1)/(0.115m)-(1)/(0.365))\\W=0.94J`

The work is positive since the potential energy in 1 is greater than 2.