Answer:
the radius of bigger loop = 6 cm
Step-by-step explanation:
given,
two concentric current loops
smaller loop radius = 3.6 cm
]current in smaller loop = 12 A
current in the bigger loop = 20 A
magnetic field at the center of loop = 0
Radius of the bigger loop = ?
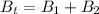
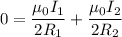
now, on solving
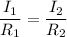
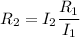
=
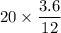
= 6 cm
hence, the radius of bigger loop = 6 cm