Question

Radium has a half-life of 1,660 years. Calculate the number of years until only 1/16th of a sample remains.

years

Answer 1

Radium has a half-life of 1,660 years.The number of years until only 1/16th of a sample remains is 6641 years.

Answer: 6641 years

Step-by-step explanation:

Given that the half-life of Radium is 1660 years. The number of years to be calculated when the sample of radium could just be remained of 1/16th of its part, which can be calculated by the following means,

Half life,
`T_(1 / 2)=1660 \text { years }`

`(N)/(N_(0))=(1)/(16)`

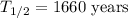
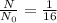
t is the taken time, then,

`(N)/(N_(0))=e^(-\lambda t)`

`(N)/(N_(0))=e^(\lambda t)`

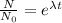
Taking ln on both sides, we get,

`\lambda t=\ln \left((N)/(N_(0))\right)`

`t=(1)/(\lambda) \ln \left((N_(0))/(N)\right)`

`=(T_(1 / 2))/(0.693)\left(\ln \left((N_(0))/(N)\right)\right)`

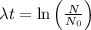
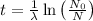
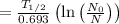
By substituting the given values,

`t = (1660)/(0.693)(\ln 16)`

Therefore, t = 6641 years