Question

In Austria, 30% of the population has a blood type of O+, 33% has A+, 12% has B+, 6% has AB+, 7% has O-, 8% has A-, 3% has B-, and 1% has AB-. If 15 Austrian citizens are chosen at random, what is the probability that 3 have a blood type of O+, 2 have A+, 3 have B+, 2 have AB+, 1 has O-, 2 have A-, 1 has B-, and 1 has AB-?

Answer 1

Answer: The probability that 3 have a blood type of O+, 2 have A+, 3 have B+, 2 have AB+, 1 has O-, 2 have A-, 1 has B-, and 1 has AB- is 0.0011%

Explanation: For calculate the probability, we have to use multinomial distribution:

P=n!
`(n!)/(n1!n2!n3!..nk!) (p1n^(1) p2n^(2)p3n^(3)..pkn^(k))`

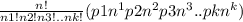
n: number of trials, p: probability for each possible outcome, k: number of possible outcomes.

The probability of each blood type are:

• P1(0+)=0.30
• P2(A+)=0.33
• P3(B+)=0.12
• P4(AB+)=0.06
• P5(0-)=0.07
• P6(A-)=0.08
• P7(B-)=0.03
• P8(AB-)=0.01

If 15 Austrian citizens are chosen at random, there are 15 trials. n=15

for n1=3 because 3 P(0+)

for n2=2 because 2 P(A+)

for n3=3 because 3 P(B+)

for n4=2 because 2 P(AB+)

for n5=1 because 1 P(0-)

for n6=2 because 2 P(A-)

for n7=1 because 1 P(B-)

for n8=1 because 1 P(AB-)

k=8 (because there are 8 possibilities)

`P=(15!)/(3!2!3!2!1!2!1!1) (0.30^(3)0.33^(2)0.12^(3)0.06^(2)0.07^(1)0.08^(2)0.03^(1)0.01^(1))`

P=0.000011

Px100=0.0011