Answer:
The probability of failure of both the bulbs is 0.4323.
Explanation:
For an exponential distribution the distribution is given by
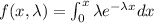
The value of λ is related to the mean μ as λ=1/μ,
Let us denote the 2 bulbs by X and Y thus the probability distribution of the 2 bulbs is as under
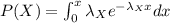
Similarly for the bulb Y the distribution function is given by
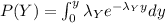
Thus the probability for both the bulbs to fail within 1500 hours is
