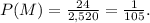Question

Suppose there are eight socks in a bag, numbered one through eight, which can be grouped into four pairs: {1,2}, {3,4}, {5,6}, or {7,8}. The socks of each pair have the same color; different pairs have different colors. Suppose there are four (distinct!) people present, and one at a time, they each draw two socks out of the bag, without replacement. Suppose all socks feel the same, so when two socks are drawn from the bag, all possibilities have equal probability. Let M be the event that each person draws a matching pair of socks. What is the number of outcomes in M?

Answer 1

The number of outcomes in event M is 96.

Step-by-step explanation:

To find the number of outcomes in event M, we need to consider the number of ways each person can draw a matching pair of socks. The first person can choose any of the 4 pairs, which gives them 2 socks. The second person can choose from the remaining 3 pairs, and so on. So, the number of outcomes in M is 4 x 2 x 3 x 2 x 2 x 1 x 1 x 1 = 96.

Answer 2

• The number of outcomes in M is 24, each one with a
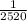  `(1)/(2520)` probability to happen.
• The probability of M to happen is
  `(1)/(105)`

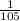
Step-by-step explanation:

There are 4 people and 4 different pairs of socks which we will denote by A,B,C and D. If every person ends with a matching pair of socks that means that:

• Person 1 ended with pair A,B,C or D. (4 possibilities).
• Person 2 ended with pair A,B,C or D, but without the pair that Person 1 has. (3 possibilities).
• Person 3 ended with pair A,B,C or D, but no with the pair person 1 has neither the one of person 2 has. (2 possibilities).
• Person 4 will end with the remaining pair of socks (1 possibility).

Therefore the numbers of outcomes of M is
`4*3*2*1=24.`

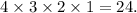
It is clear that each one of those outcomes have the same probability to happen. Then we will compute the probability of one of them (which we will denote as
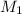`M_1`) and then multiply by 24 to obtain the probability of M.

We will compute the probability of:

• Person 1 choosing pair A={1,2}
• Person 2 choosing pair B={3,4}
• Person 3 choosing pair C={5,6}
• Person 4 choosing pair D={7,8}

Without loss of generality we will assume that person 1 chooses first, then person 2 and so on.

Observe that the number of ways of choosing 2 socks is given by:

`{{8} \choose {2}} = (8!)/(6!2!)=(8*7)/(2)=28`

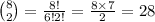
Therefore, the probability of person 1 to choose the pair A={1,2} is
`(1)/(28)`.

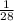After that, there would remain 6 socks in the bag. Then, the probability of person 2 of choosing pair B={3,4} is 1 in
`{6 \choose2}=(6!)/(4!2!)=(6*5)/(2)=15.`. That is
`(1)/(15).`

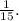
After that, there would remain 4 socks in the bag. Then, the probability of person 3 of choosing pair C={5,6} is 1 in
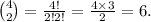`{4 \choose2}=(4!)/(2!2!)=(4*3)/(2)=6.`. That is
`(1)/(6).`

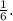
Finally when person 4 chooses, there would be only 2 socks (pair D={7,8}) so, the probability of choosing pair D is 1.

Therefore, the probability of
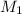`M_1` to happen is

`P(M_1)=(1)/(28) * (1)/(15) *(1)/(6)* 1=(1)/(2,520).`

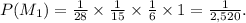
And in consequence

`P(M)=(24)/(2,520)=(1)/(105).`