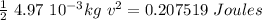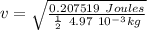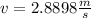Question

A spring gun is made by compressing a spring in a tube and then latching the spring at the compressed position. A 4.97-g pellet is placed against the compressed and latched spring. The spring latches at a compression of 4.60 cm, and it takes a force of 9.12 N to compress the spring to that point. (Note: while the spring is being compressed the ball is not in contact with the spring.) (a) If the gun is fired vertically, how fast is the pellet moving when it loses contact with the spring? (Include the effect of gravity and assume that the pellet leaves the spring when the spring is back to its relaxed length.)

Answer 1

`v  = 2.8898 (m)/(s)`

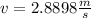
Step-by-step explanation:

This is a problem easily solve using energy conservation. As there are no non-conservative forces, we know that the energy is conserved.

When the spring is compressed downward, the spring has elastic potential energy. When the spring is relaxed, there is no elastic potential energy, but the pellet will have gained gravitational potential energy and kinetic energy. Lets see what are the terms for each of this.

Elastic potential energy

We know that a spring following Hooke's Law has a elastic potential energy:

`E_(ep) = (1)/(2) k (\Delta x)^2`

where
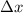`\Delta x` is the displacement from the relaxed length and k is the spring's constant.

To obtain the spring's constant, we know that Hooke's law states that the force made by the spring is :

`\vec{F} = - k \Delta \vec{x}`

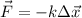
as we need 9.12 N to compress 4.60 cm, this means:

`k = (9.12 \ N)/(4.6 \ 10^(-2) \ m)`

`k = 198.26 \ ( N)/(m)`

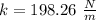
So, the elastic energy of the compressed spring is:

`E_(ep) = (1)/(2) 198.26 \ ( N)/(m) (4.6 \ 10^(-2) \ m)^2`

`E_(ep) = 0.209759 \ Joules`

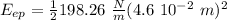
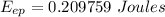
And when the spring is relaxed, the elastic potential energy will be zero.

Gravitational potential energy

To see how much gravitational potential energy will the pellet win, we can use

`\Delta E_(gp) = m g \Delta h`

where m is the mass of the pellet, g is the acceleration due to gravity and \Delta h is the difference in height.

Taking all this together, the gravitational potential energy when the spring is relaxed will be:

`\Delta E_(gp) = 4.97 \ 10^(-3) kg \ 9.8 (m)/(s^2) 4.6 \ 10^(-2) m`

`\Delta E_(gp) = 0.00224 \ Joules`

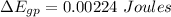
Kinetic Energy

We know that the kinetic energy for a mass m moving at speed v is:

`E_k = (1)/(2) m v^2`

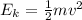
so, for the pellet will be

`E_k = (1)/(2) \ 4.97 \ 10^(-3) kg \ v^2`

All together

By conservation of energy, we know:

`E_(ep) = \Delta E_(gp) + E_k`

`0.209759 \ Joules = 0.00224 \ Joules + (1)/(2) \ 4.97 \ 10^(-3) kg \ v^2`

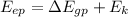
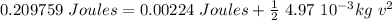
So

`(1)/(2) \ 4.97 \ 10^(-3) kg \ v^2  = 0.209759 \ Joules - 0.00224 \ Joules`

`(1)/(2) \ 4.97 \ 10^(-3) kg \ v^2  = 0.207519 \ Joules`

`v  = \sqrt{ ( 0.207519 \ Joules)/( (1)/(2) \ 4.97 \ 10^(-3) kg ) }`

`v  = 2.8898 (m)/(s)`