Question

A rectangular steel plate expands as it is heated. Find the rate of change of area with respect to temperature T when the width is 1.6 cm and the length is 2.8 cm if d l divided by dt equals 1.9 times 10 Superscript negative 5 Baseline cm divided by degrees Upper C and dw divided by dt equals 8.5 times 10 Superscript negative 6 Baseline cm divided by degrees C. Round to one decimal place.

Answer 1

To find the rate of change of the area of a steel plate with respect to temperature, we multiply the rates of expansion for width and length by their respective dimensions and sum them up. This yields the total rate of change of the area based on the given rates of expansion for each dimension.

Step-by-step explanation:

The question requires us to find the rate of change of the area of a steel plate with respect to temperature (T) during thermal expansion when certain dimensions and rates of change are given. The formula to find the change in area due to thermal expansion for small temperature changes is ΔA = 2αΔAT. Given that the width (w) and length (l) of the plate are 1.6 cm and 2.8 cm respectively, and the rate of change with respect to temperature for the width and length are 8.5 × 10-6 cm/°C and 1.9 × 10-5 cm/°C, the rate of change of the area is calculated using the formula for the area of a rectangle, A = l × w, and taking its derivative with respect to temperature, dA/dT. Incorporating the given rates, the solution becomes:

• First, calculate the rate of change of area with respect to temperature (dA/dT) for both dimensions.
• Multiplying the rates of change for length and width by their respective dimensions to find the total rate of change of the area.

The calculation would be: dA/dT = dl/dT × w + dw/dT × l = (1.9 × 10-5 × 1.6) + (8.5 × 10-6 × 2.8). After calculating and rounding to one decimal place, we find the rate of change of the area with respect to temperature.

Answer 2

The variation rate is 5.42 10⁻⁵ cm²/ºC

Step-by-step explanation:

When we have a thermal expansion problem we must have the relationship of the change in length as a function of the temperature, which are given in this problem, so we can write the expression for the area of ​​a rectangle

a = L W

They ask us to find the rate of variation of this area depending on the temperature, so we can derive this expression with respect to the temperature

da / dT = d(LW) / dt

We use the derivative of a product since the two magnitudes change

da / dT = W dL/dT + L dW/dT

The values ​​they give us are

`(dL)/(dT)` = 1.9 10⁻⁵ cm/ºC

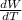`(dW)/(dT)` = 8.5 10⁻⁶ cm/ºC

W = 1.6 cm

L= 2.8 cm

Substituting the values ​​and calculating

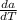`(da)/(dT)` = 1.6 1.9 10⁻⁵ + 2.8 8.5 10⁻⁶

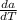`(da)/(dT)` = 3.04 10⁻⁵ + 2.38 10⁻⁵

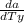`(da)/(dTy)`= 5.42 10⁻⁵ cm²/ºC

The variation rate is 5.42 10⁻⁵ cm²/ºC