Question

A small Styrofoam bead with a charge of −60.0 nC is at the center of an insulating plastic spherical shell with an inner radius of 20.0 cm and an outer radius of 24.0 cm. The plastic material of the spherical shell is charged, with a uniform volume charge density of −2.05 µC/m3. A proton moves in a circular orbit just outside the spherical shell. What is the speed of the proton (in m/s)?

Answer 1

speed of the proton is 6.286 ×
`10^(5)` m/s

Step-by-step explanation:

given data

charge q= −60.0 nC

inner radius a = 20.0 cm

outer radius b = 24.0 cm

charge density ρ = −2.05 µC/m³

to find out

What is the speed of the proton

solution

we know that force on the proton due to this electric field is express as

F = q × E ...................1

here F is force and q is charge and E is electric filed so

if v be the speed of the proton in circular orbit than force will be

F =
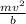`(mv^2)/(b)` ....................2

from equation 1 and 2

q × E =
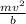`(mv^2)/(b)` .......................3

so

here total charge Q on shell is

Q = ρ × V

here ρ is density and V is volume

Q =
`\rho * (4)/(3) \pi  (b^3-a^3)`

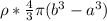
put here value

Q =
`-2.05*10^(-6) (4)/(3) \pi  (0.24^3-0.20^3)`

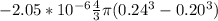
Q = 50.01 ×
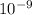`10^(-9)` C

and

total charge enclosed by Gaussian surface is

qin = q + Q

qin = −60 ×
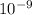`10^(-9)` C - 50.01 ×
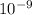`10^(-9)` C

qin = - 110.01 ×
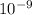`10^(-9)` C

and

from Gauss law

`\oint E*A = (\left | qin \right | )/(\epsilon )`

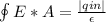
E ×4×π×b² =
`(110.01*10^(-9) )/(\epsilon )`

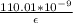
E =
`(110.01*10^(-9) )/(\epsilon *4 *\pi *b^2[tex])`

E =
`(9*10^9 * 110.01*10^(-9) )/(0.24^2)`

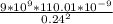
E = 17189.06 N/C

so

from equation 3

q × E =
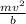
`(mv^2)/(b)`

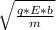
v =
`\sqrt{(q*E*b)/(m)}`

v =
`\sqrt{(1.6*10^(-19)*17189.06*0.24)/(1.67*10^(-27))}`

v = 6.286 ×
`10^(5)` m/s

so speed of the proton is 6.286 ×
`10^(5)` m/s