Answer:
The compression is
 .
.
Step-by-step explanation:
A Hooke's law spring compressed has a potential energy
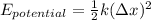
where k is the spring constant and
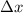 the distance to the equilibrium position.
the distance to the equilibrium position.
A mass m moving at speed v has a kinetic energy
 .
.
So, in the first part of the problem, the spring is compressed a distance d, and then launch the mass at velocity
 . Knowing that the energy is constant.
. Knowing that the energy is constant.
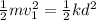
If we want to double the kinetic energy, then, the knew kinetic energy for a obtained by compressing the spring a distance D, implies:
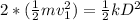
But, in the left side we can use the previous equation to obtain:
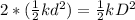
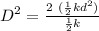
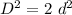
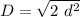
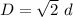
And this is the compression we are looking for