Answer:
Confidence interval = ( 0.7991, 0.8647 )
Explanation:
Sample size = n = 351
number of successes = X = 292
Sample proportion = P =
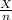
=
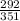
= 0.831908831
confidence interval = 90%
Critical Z value = 1.6449 [by using excel]
Confidence interval = P ± Z
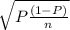
Where P = Sample proportion
Z = critical value
n = sample size
Confidence interval = 0.831908831 ± 1.6449
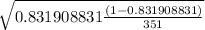
= 0.831908831 ± 1.6449 × 0.0200
= 0.831908831 ± 0.032898
Lower limit = 0.831908831 - 0.032898 = 0.7991
Upper limit = 0.831908831 + 0.032898 = 0.8647
Confidence interval = ( 0.7991, 0.8647 )