Question

Police response time to an emergency call is the difference between the time the call is first received by the dispatcher and the time a patrol car radios that it has arrived at the scene. Over a long period of time, it has been determined that the police response time has a normal distribution with a mean of 8.8 minutes and a standard deviation of 1.9 minutes. For a randomly received emergency call, find the following probabilities. (a) the response time is between 5 and 10 minutes

(b) the response time is less than 5 minutes


(c) the response time is more than 10 minutes

Answer 1

`\mu = 8.8\\\sigma = 1.9`

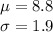
Now we are supposed to find probabilities that the response time is between 5 and 10 minutes i.e P(5<x<10)

Formula :
`z= (x-\mu)/(\sigma)`

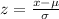
at x = 5

`z= (5-8.8)/(1.9)`

`z=-2`

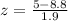
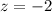
at x = 10

`z= (10-8.8)/(1.9)`

`z=0.6315`

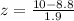
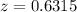
P(-2<z<0.6315)=P(z<0.6315)-P(z<-2)

Refer the z table

P(-2<z<10)=0.7357-0.0228=0.7129

So, the probability that response time is between 5 and 10 minutes is 0.7129

b)the response time is less than 5 minutes

at x = 5

`z= (5-8.8)/(1.9)`

`z=-2`

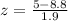
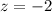
P(x<5)=P(z<-2)=0.0228

So, the probability that the response time is less than 5 minutes is 0.0228

c)the response time is more than 10 minutes

at x = 10

`z= (10-8.8)/(1.9)`

`z=0.6315`

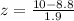
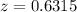
P(x>10) = 1-P(x<10) = 1-P(z<0.63) = 1-0.7357 = 0.2643

So, The probability that the response time is more than 10 minutes is 0.2643