Answer:
Explanation:
Assuming that the differential equation is
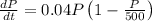 .
.
We need to solve it and obtain an expression for
 in order to complete the exercise.
in order to complete the exercise.
First of all, this is an example of the logistic equation, which has the general form
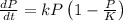 .
.
In order to make the calculation easier we are going to solve the general equation, and later substitute the values of the constants, notice that
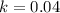 and
and
 and the initial condition
and the initial condition
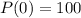 .
.
Notice that this equation is separable, then
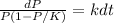 .
.
Now, intagrating in both sides of the equation
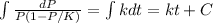 .
.
In order to calculate the integral in the left hand side we make a partial fraction decomposition:
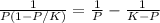 .
.
So,
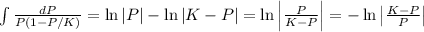 .
.
We have obtained that:
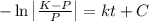
which is equivalent to
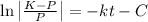
Taking exponentials in both hands:

Hence,
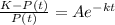 .
.
The next step is to substitute the given values in the statement of the problem:
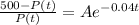 .
.
We calculate the value of
 using the initial condition
using the initial condition
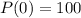 , substituting
, substituting
 :
:
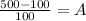 and
and
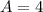 .
.
So,
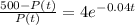 .
.
Finally, as we want the value of
 such that
such that
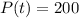 , we substitute this last value into the above equation. Thus,
, we substitute this last value into the above equation. Thus,
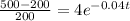 .
.
This is equivalent to
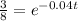 . Taking logarithms we get
. Taking logarithms we get
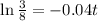 . Then,
. Then,
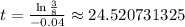 .
.
So, the population of rats will be 200 after 25 months.