Answer:
The probability that no more than more than 11 of them need correction for their eyesight is 0.00512
No, 11 is not a significantly low low number of adults requiring eyesight correction .
Explanation:
A survey showed that 77% of adults need correction for their eyesight.
If 22 adults are randomly selected, find the probability that no more than more than 11 of them need correction for their eyesight.
n =22
p = 0.77
q = 1-p = 1- 0.77=0.23
We are supposed to find
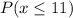
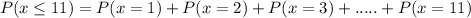
Formula :
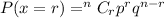
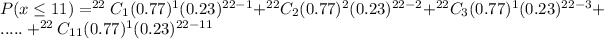
Using calculator
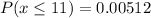
So, The probability that no more than more than 11 of them need correction for their eyesight is 0.00512
No, 11 is not a significantly low low number of adults requiring eyesight correction .