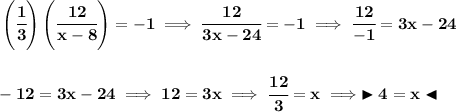Question

Line m contains the points A(-2,6) and B(4,8) while line n contains the C(8,12) and D(x,24) given m and n are perpendicular lines solve for the value of x given m and n are parallel lines solve for the value of x in your final answer include all formulas necessary to solve for x

Answer 1

tis noteworthy that perpendicular lines have negative reciprocal slopes, so if one say have a slope of a/b, the other has a slope of -b/a, so that, if we multiply both (a/b) * (-b/a) we get -1 as their product, that said, let's take a peek of the slopes of "n" and "m".

`\bf A(\stackrel{x_1}{-2}~,~\stackrel{y_1}{6})\qquad B(\stackrel{x_2}{4}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{8}-\stackrel{y1}{6}}}{\underset{run} {\underset{x_2}{4}-\underset{x_1}{(-2)}}}\implies \cfrac{2}{4+2}\implies \cfrac{2}{6}\implies \boxed{\cfrac{1}{3}} \\\\[-0.35em] ~\dotfill`

`\bf C(\stackrel{x_1}{8}~,~\stackrel{y_1}{12})\qquad D(\stackrel{x_2}{x}~,~\stackrel{y_2}{24}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{24}-\stackrel{y1}{12}}}{\underset{run} {\underset{x_2}{x}-\underset{x_1}{8}}}\implies \boxed{\cfrac{12}{x-8}}`

and well, since we know they're perpendicular

`\bf \left( \cfrac{1}{3} \right)\left( \cfrac{12}{x-8} \right)=-1\implies \cfrac{12}{3x-24}=-1\implies \cfrac{12}{-1}=3x-24 \\\\\\ -12=3x-24\implies 12=3x\implies \cfrac{12}{3}=x\implies \blacktriangleright 4 = x\blacktriangleleft`