Question

In a​ study, 36​% of adults questioned reported that their health was excellent. A researcher wishes to study the health of people living close to a nuclear power plant. Among 1111 adults randomly selected from this​ area, only 3 reported that their health was excellent. Find the probability that when 1111 adults are randomly​ selected, 3 or fewer are in excellent health. Round to three decimal places.

Answer 1

0.3907

Explanation:

We are given that 36​% of adults questioned reported that their health was excellent.

Probability of good health = 0.36

Among 11 adults randomly selected from this​ area, only 3 reported that their health was excellent.

Now we are supposed to find the probability that when 11 adults are randomly​ selected, 3 or fewer are in excellent health.

i.e.
`P(x\leq 3)=P(x=1)+{P(x=2)+P(x=3)`

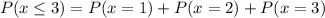
Formula :
`P(x=r)=^nC_r p^r q ^ {n-r}`

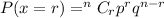
p is the probability of success i.e. p = 0.36

q = probability of failure = 1- 0.36 = 0.64

n = 11

So,
`P(x\leq 3)=P(x=1)+{P(x=2)+P(x=3)`

`P(x\leq 3)=^(11)C_1 (0.36)^1 (0.64)^(11-1)+^(11)C_2 (0.36)^2 (0.64)^(11-2)+^(11)C_3 (0.36)^3 (0.64)^(11-3)`

`P(x\leq 3)=(11!)/(1!(11-1)!) (0.36)^1 (0.64)^(11-1)+(11!)/(2!(11-2)!)  (0.36)^2 (0.64)^(11-2)+(11!)/(3!(11-3)!) (0.36)^3 (0.64)^(11-3)`

`P(x\leq 3)=0.390748`

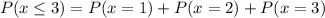
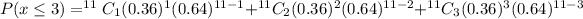
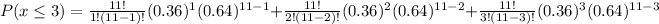
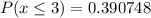
Hence the probability that when 11 adults are randomly​ selected, 3 or fewer are in excellent health is 0.3907