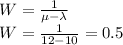Question

Customers arrive at a bank drive-up window every 6 minutes based on a Poisson distribution. Once they arrive at the teller, service time is exponentially distributed based on a rate of 5 minutes per transaction,a.What is the probability that 3 or fewer customers will arrive in one hour?b.How many customers are most likely in line (waiting) at any one point in time?c.What will be the average time waiting in the system?d.What will be the average time in the system?

Answer 1

(a) 0.01029 (b) 4.167 customers (c) 0.4167 hours or 25 minutes (d) 0.5 hours or 30 minutes

Explanation:

With an arrival time of 6 minutes, λ=10 clients/hour.

With a service time of 5 minutes per transaction, μ=12 transactions/hour.

(a) The probability of 3 or fewer customers arriving in one hour is

P(C<=3)=P(1)+P(2)+P(3)

`P(X)=\lambda^(X)*e^(-\lambda)  /X!`

`P(1)=10^(1)*e^(-10)  /1!=0.00045\\P(3)=10^(3)*e^(-10)  /3!=0,00227\\P(2)=10^(2)*e^(-10)  /2!=0,00757\\P(x\leq3)=0.00045+0.00227+0.00757 = 0.01029`

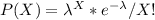
(b) The average number of customers waiting at any point in time (Lq) can be calculated as

`L_(q)=p*L=(\lambda)/(\mu)*(\lambda)/(\mu-\lambda)\\L_(q)=(10)/(12)*(10)/(12-10)\\\\L_(q)=100/24=4.167`

(c) The average time waiting in the system (Wq) can be calculated as

`W_(q)=p*W=(\lambda)/(\mu)*(1)/(\mu-\lambda)\\W_(q)=(10/12)*(1/(12-10))\\W_(q)=(10/24)=0.4167`

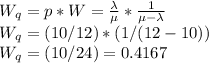
(d) The average time in the system (W), waiting and service, can be calculated as

`W=(1)/(\mu-\lambda)\\W=(1)/(12-10)=0.5`