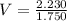Answer:
Displacement: 2.230 km Average velocity: 1.274
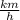
Step-by-step explanation:
Let's represent displacement by the letter S and the displacement in direction 49.7° as A. Displaement is a vector, so we need to decompose all the bird's displacement into their X-Y compoments. Let's go one by one:
- 0.916 km due east is an horizontal direction and cane be seen as direction towards the negative side of X-axis.
- 0.928 km due south is a vertical direction and can be seen as a direction towards the negative side of Y-axis.
- 3.52 km in a direction of 49.7° has components on X and Y axes. It is necessary to break it down using trigonometry,
First of all. We need to sum all the X components and all the Y componets.
∑
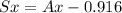 ⇒ ∑
⇒ ∑
![Sx = [tex]3.52cos(49.7) - 0.916](https://img.qammunity.org/2020/formulas/physics/high-school/1nw46fquyi1llhesfb92h2qnmfdhwf4e6l.png)
∑
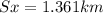
∑
 ⇒ ∑
⇒ ∑
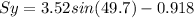
∑
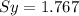
The total displacement is calculated using Pythagoeran therorem:
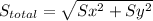 ⇒
⇒
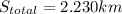
With displacement calculated, we can find the average speed as follows:
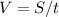 ⇒
⇒