Question

For the month of March in a certain​ city, 57​% of the days are cloudy. Also in the month of March in the same​ city, 55​% of the days are cloudy and foggy. What is the probability that a randomly selected day in March will be foggy if it is cloudy​?

Answer 1

P(F | C) = 0.96

Explanation:

Hi!

This is a problem on conditional probability. Lets call:

C = { cloudy day }

F = { foggy day }

Then F ∩ C = { cloudy and foggy day }

You are asked for P(F | C), the probability of a day being foggy given it is cloudy. By definition:

`P(F|C)=(P(F\bigcap C))/(P(C))`

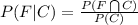
And the data you have is:

`P(C) = 0.57\\P(F \bigcap C) =0.55`

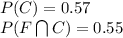
Then: P(F | C) = 0.96