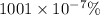Question

transmission channel operates at 3Mbps and has a bit error rate of 10^(-3). Bit errors occur at random and independent of each other. Suppose that the following code is used. To transmit a 1, the codeword 111 is sent; to transmit a 0, the codeword 000 is sent. The Receiver takes the three received bits and decides which bit was sent by taking the majority vote of the three bits. Find the probability that the receiver makes a decoding error.

Answer 1

`1001* 10^(-7)\%`

Explanation:

The receiver makes a decoding error only if three bits or two bits of a 3-bit string are sent wrongly.

Let's call

p = probability that one bit was sent incorrectly.

Since bit errors occur random and independently of each other, the probability that 3 bits are sent incorrectly is

`p* p* p=p^3`

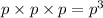
Similarly, the probability that 2 bits are sent incorrectly is

`p* p=p^2`

The probability that 3 or 2 bits are sent incorrectly is

`p^3+p^2`

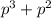
So, all we have to do now is compute p.

Let x be the number of bits incorrectly transmitted per unit of time.

Since the channel operates at 3 Mbps (3,000,000 bits per second) and has a bit error rate of 0.001, then

`BitErrorRate=(errors)/(total bits)=(x)/(3,000,000)=0.001`

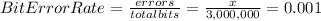
and

x = 3000

This means that for every 3 million bits transmitted, 3000 are wrong.

So, the probability p that one bit is incorrect when transmitted is

`p=(3000)/(3,000,000)=0.001`

(Remark: When the probability is measured as a number between 0 and 1, it can be shown that the bit error rate and the probability of sending one bit incorrectly are the same)

Hence the probability that the receiver makes a decoding error is

`0.001^3+0.001^2=1001* 10^(-9)`

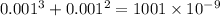
or in % notation

`1001* 10^(-7)\%`