Question

What is the apparent density of a barrel filled with air. The barrel is in the shape of a perfect cylinder with a height of 88.9 cm, a diameter of 61.0 cm, and a wall thickness of 3.67 mm. The barrel is made of steel. The density of steel is 7.85 g/cm3 and the density of air is 1.292 g /L. Will the barrel float on water or sink?

Answer 1

Answer: Yes, the barrel will float

Explanation:

To calculate if the barrrel will float or not, we need to know if the barrel's density while filled with air is less or more than water.

To calculate density, we use the following formula:

Density (D) = Mass (m) / Volume (v)

Where mass are equals to the sum of the mass of air and steel.

m = Steel's Mass (ms) + Air's Mass (ma)

And the Volume is very easy to calculate with the data already given, and this formula:

Cylinder Volume = Cylinder's Height * π
`radius^(2)`

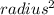
Where the Radius can be know by dividing the Diameter in two:

Diameter = radius * 2

radius = Diameter / 2

radius = 61cm / 2

radius = 30.5 cm

Knowing this:

Cylinder Volume = 88.9 cm * π
`30.5 cm^(2)`

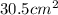
Cylinder's Volume = 82699.225
`cm^(3)`

Also, knowing formula, it can be calculated the volume and mass for the air inside, by taking in mind the barrel thickness. The thickness will be subtracted from the radius and two times from the height. So, the volumen of air will be equals to:

va = (88.9 cm - 2*0.367 cm) *π
`(30.5-0.367)^(2)`

va = 88.166 *π
`(30.133)^(2)`

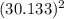
va = 251498.705
`cm^(3)`

With the volume of air, know we can calculate how much mass there is, this because:

Density (D) = Mass (M) / Volume (V)

M = D * V

Then

ma = da * va

ma = 1.292 g/L * 80054.524
`cm^(3)`

In this case we have to take in consideration, that the volume found and the density given are not on the same units, so we can do the following:

1 Liter (L) = 1000
`cm^(3)`

Knowing this, we can use this new value in our equation to calculate the Air's Mass:

ma = (1.292 g/ 1000
`cm^(3)` ) * 80054.524
`cm^(3)`

ma = 103.430 g

The Air's Mass is knowwed.

For Steel we know that is a empty barrel, with a wall thickness equals to 3.67mm. With this in mind we need to calculate the total volume of Steel. In this case it can be though of the barrel is conformed by two cilinder on the top (the barrel's two covers) and the barrel body.

For the two covers, their volumen can be calculated by knowing the radius and the thickness, the thickness will be how tall whis cilinder is.

Cover's Volume = Barrel's Thickness * π
`Barrel's radius^(2)`

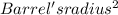
Cover's Volume = 0.0367 cm * π
`Barrel's radius^(2)`

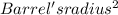
Cover's Volume = 107.254
`cm^(3)`

The barrels body can be though as a long ring. To calculate his volumen we need to know the barrels height, which is know and the area of the ring.

The area of the ring can be though as substraction of the area occupy by the circle created by the Internal Radius to the total circle create by the Cylinder.

Ring's Area = Cylinder's Circle Area - Internal's Circle Area

Ring's Area = π
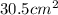`30.5 cm^(2)` - π
`(30.5 cm-0.00367)^(2)`

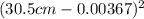
Ring's Area = 0.703
`cm^(2)`

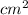
WIth the RIng's Area, it can be know the volume:

Ring's Volume = Ring's Area * Height

RIng's Volume = 0.703
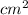`cm^(2)` * 88.9cm

Ring's Volume = 62.521
`cm^(3)`

Know by adding the volume of the two covers and the ring we can know the total steel volume of the barrel.

Steel's Volume = Upper Cover + Lower Cover + Barrel's Body

Steel's Volume = 107.254
`cm^(3)` + 107.254
`cm^(3)`+ 62.521
`cm^(3)`

Steel's Volume = 277.029
`cm^(3)`

We can finally can calculate the Barrel's total Steel Mass, the same way we calculate with air

ms = Steel's Volume* Steel's Density

ma = (7.85 g/
`cm^(3)` ) * 277.029
`cm^(3)`

ms = 2174.677 g

With the Steel's Mass finally calculated, we can know how much mass is on the barrel

m = ms + ma

m = 2174.677 g + 103.430 g

m = 2278.107 g

With the full mass of the barrel, we can calculate the barrel's density

D = m / v

D = 2278.107 g / (82699.225
`cm^(3)`)

D = 0.02754
`g/cm^(3)`

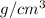
For the barrel to float, the density should be less than water:

Water's Density = 1000 Kg/
`m^(3)`

By changing this units:

Water's Density = 1 g/(
`cm^(3)`)

By this, we can see that the Water is more dense that the full barrel, because of this, the Barrel will float