Question

An 800 kHz radio signal is detected at a point 2.1 km distant from a transmitter tower. The electric field amplitude of the signal at that point is 800 mV/m. Assume that the signal power is radiated uniformly in all directions and that radio waves incident upon the ground are completely absorbed. The intensity of the radio signal at that point is closest to

Answer 1

`I=8.48* 10^(-4)\ W/m^2`

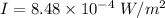
Step-by-step explanation:

Given that,

Frequency of the radio signal,
`f=800\ kHz=8* 10^5\ Hz`

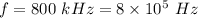
It is detected at a pint 2.1 km from the transmitter tower, x = 2.1 km

The amplitude of the electric field is, E = 800 mV/m

Let I is the intensity of the radio signal at that point. Mathematically, it is given by :

`I=(E^2_(rms))/(c\mu_o)`

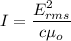
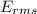`E_(rms)` is the rms value of electric field,
`E_(rms)=(E)/(√(2) )`

`I=(E^2)/(2c\mu_o)`

`I=((800* 10^(-3))^2)/(2* 3* 10^8* 4\pi * 10^(-7))`

`I=8.48* 10^(-4)\ W/m^2`

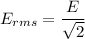
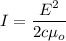
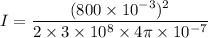
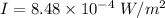
So, the intensity of the radio signal at that point is
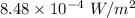`8.48* 10^(-4)\ W/m^2`. Hence, this is the required solution.