Question

Electric charge is uniformly distributed inside a nonconducting sphere of radius 0.30 m. The electric field at a point P, which is 0.50 m from the center of the sphere, is 15,000 N/C and is directed radially outward. What is the maximum magnitude of the electric field due to this sphere?

Answer 1

`E_(max)=41666.66\ N/C`

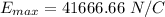
Step-by-step explanation:

Given that,

The radius of sphere, r = 0.3 m

Distance from the center of the sphere to the point P, x = 0.5 m

Electric field at point P,
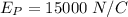`E_P=15000\ N/C` (radially outward)

The maximum electric field is at the surface of the sphere. We know that the electric field is inversely proportional to the distance. So,

`(E_(max))/(E_p)=(0.5^2)/(0.3^2)`

`(E_(max))/(15000)=(0.5^2)/(0.3^2)`

`{E_(max)}=(0.5^2)/(0.3^2)* 15000`

`E_(max)=41666.66\ N/C`

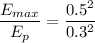
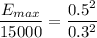
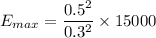
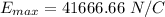
So, the magnitude of the electric field due to this sphere is 41666.66 N/C. Hence, this is the required solution.