Question

7 men and 3 women are ranked according to their scores on an exam. Assume that no two scores are alike, and that all 10! possible rankings are equally likely. Let X denote the highest ranking achieved by a man (so X=1 indicates that a man achieved the highest score on the exam). Find each of the following: P(X=1)= P(X=2)= P(X=3)= P(X=6)=

Answer 1

P(X=1)=0.7 P(X=2)=0.233 P(X=3)=0.058 P(X=6)=0

Explanation:

P(X=1) means that a man achieved the highest score.

7 out of 10 possible combinations have a man with the highest score, so P(X=1)=0.7.

P(X=2)

In this case, we have a woman in the first place and a man in the second place.

We have 3 combinations for the first place and 7 for the second place, out of 10!/(10-2)! possible combinations for the first and second place.

We can calculate P(X=2) as

`P(x=2)=(3*7)/(10!/8!)=21/(10*9)=21/90 =  0.233`

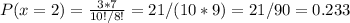
P(X=3)

In this case, we have two women in the first and second place, and a man in the 3rd place.

We have 3*2 combinations for the 1st and 2nd places and 7 combinations for the 3rd place, out of 10!(10-3)! possible combinations for the 1st,2nd and 3rd places.

We can calculate P(X=3) as

`P(x=3)=(3*2*7)/(10!/7!)=42/(10*9*8)=42/ 720=  0.058`

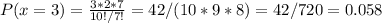
P(X=6)

In this case, we can say P(X=6) because there is only 3 women in the sample, so X must be 4 or smaller (P(X>4)=0).