Question

Suppose you have two identical capacitors. You connect the first capacitor to a battery that has a voltage of 21.2 volts, and you connect the second capacitor to a battery that has a voltage of 12.8 volts. What is the ratio of the energies stored in the capacitors?

Answer 1

r=2.743

Step-by-step explanation:

The energy stored on a capacitor is of type potencial, therfore depends on the capacity to "store" energy. Inthe case of the capacitor, it stores charge (Q), and the equations you use to calculate it are:

`E_p=(Q^2)/(2C)=(QV)/(2)=(CV^2)/(2)`

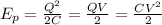
In this case we know V and C, therefore we use the last expression:

`E_(p1)=(CV_1^2)/(2)`

`E_(p2)=(CV_2^2)/(2)`

`(E_(p1))/(E_(p2))=r=((CV_1^2)/(2))/((CV_2^2)/(2))  \\r=((V_1)/(V_2))^2\\r=((21.2)/(12.8))^2`

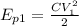
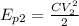
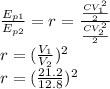
r=2.743