Question

The velocity of a car over the time period 0≤t≤3 is given by the function v(t)=60te−t4 miles per hour, where t is time in hours. What was the distance the car traveled in the first 120 years? Set up the integral to solve the problem and round your answer to two decimal places.

Answer 1

For 120 year (1051200 hours), we don´t know which function give us the velocity of the car because it is stated on the question that
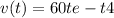`v(t)= 60te-t4` is only valid for the first 3 hours.

I assume you mistake 120 years with 120 minutes (2 hours). If this is the case, then the question can be solve.

Answer (For 120 minutes):

First, we need to have the same unit in for our variable and for the domain of the function. It can be done by change 120 to hours or changing t from 0 to 3 to minutes.

The easiest way is doing
`120 min * (1h)/(60min) = 2h`

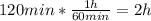
Having the variable and the domain in the same unit, allow us to solve this problem as a kinematics problem.

You may know that velocity is equal to the varion of space over time.

mathematically, that means:

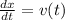`(dx)/(dt) = v(t)`. If we know the function v(t), we can obtain x(t) by solving this equality as a differential equation.

`(dx)/(dt) = v(t)\\\\dx=v(t) dt\\\\\\\int\limits^A_B {} \, dx = \int\limits^a_b {v(t)} \, dt`

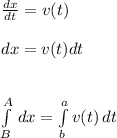
Before jumping into the integral, we need to determine the integration point A-B and a-b.

As the question ask for a the distain between two points, we can assume the first point is x0=0 and the last point is xf=d, where d represents the travelled distance. So A-B=0-d.

For a-b, the question ask for a 2 hours trip. So we adding the velocity from the hour zero to the hour 2. So a-b=0-2.

`\\\int\limits^d_0 {} \, dx = \int\limits^2_0 {v(t)} \, dt\\\\ v(t)= 60te-t4\\\\\\\int\limits^d_0 {} \, dx = \int\limits^2_0 {60te-t4} \, dt\\\\\\d= \int\limits^2_0 {60te} \, dt  +  \int\limits^2_0 {-t4} \, dt\\d= 60e \int\limits^2_0 {t} \, dt - 4  \int\limits^2_0 {t} \, dt\\d= 60 e ((2^(2)-0) )/(2) -4  ((2^(2)-0) )/(2) = 60e*2 - 4*2=120e-8.`

So the travelled distance d is 318,19 miles.