Question

A gas in a piston–cylinder assembly undergoes a compression process for which the relation between pressure and volume is given by pVn = constant. The initial volume is 0.1 m3 , the final volume is 0.04 m3 , and the final pressure is 2 bar. Determine the initial pressure, in bar, and the work for the process, in kJ, if (a) n = 0, (b) n = 1, (c) n = 1.3

Answer 1

A) P1=2 [bar] , W=-12 [kJ]

B) P1=0.8 [bar] , W=-7.3303 [kJ]

C) P1=0.6077 [bar] , W=-6.4091 [kJ]

Step-by-step explanation:

First, from the problem we know the following information:

V1=0.1 m^3

V2=0.04 m^3

P2=2 bar =200 kPa

The relation PV^n=constant means PV^n is a constant through all the process, so we can derive the initial pressure as:

`P_(1)V^(n) _(1)= P_(2)V^(n) _(2)`

`P_(1)= (P_(2)V^(n) _(2))/(V^(n) _(1))`

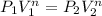
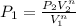
a) To the case a) the constant n is equal to 0, we can calculate the initial pressure substituting n=0 in the previous expression, so:

`P_(1)= (P_(2)V^(n) _(2))/(V^(n) _(1))=((200 kPa)(0.04 m^(3))^(0) )/((0.1 m^(3))^(0) )=200 kPa=<strong>2 bar</strong>`

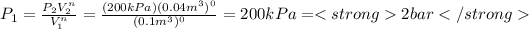
The expression to calculate the work is:

`W=\int\limits^2_1 {P} \, dV`

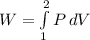
If n=0:

`P_(1)V_(1)^0 =P_(2)V_(2)^0 \\P_(1)=P_(2)`

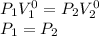
Then:

`W=\int\limits^2_1 {P} \, dV=P\int\limits^2_1 {} \, dV=P(V_(2)-V_(1))`

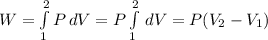
The work is:

`W=P(V_(2)-V_(1))=(200 kPa)(0.04 m^3 -0.1 m^3)=-12 (kPa)(m^3)=<strong>-12kJ</strong>`

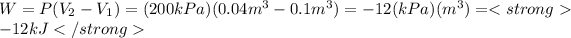
b) To the case b) the constant n is equal to 1, we can calculate the initial pressure substituting n=1 in the initial expression, so:

`P_(1)= (P_(2)V^(n) _(2))/(V^(n) _(1))=((200 kPa)(0.04 m^(3))^(1) )/((0.1 m^(3))^(1) )=80 kPa=<strong>0.8 bar</strong>`

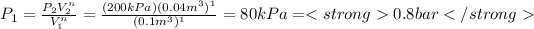
If n=1 then:

`P_(1)V_(1)^1 =P_(2)V_(2)^1 \\P_(1)V_(1) =P_(2)V_(2)=constant`

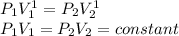
To calculate the work:

`[tex]W=constant\int\limits^2_1 {(1)/(V) } \, dV`[/tex]

`W=(constant)ln((V_(2))/(V_(1) ) )=PVln((V_(2))/(V_(1) ) )`

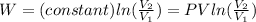
Substituting:

`W=(80kPa)(0.1 m^3)ln((0.04 m^3)/(0.1m^3 ) )=<strong>-7.3303kJ</strong>`

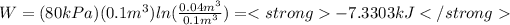
c) To the case c) the constant n is equal to 1.3, we can calculate the initial pressure substituting n=1.3 in the initial expression, so:

`P_(1)= (P_(2)V^(n) _(2))/(V^(n) _(1))=((200 kPa)(0.04 m^(3))^(1.3) )/((0.1 m^(3))^(1.3) )=60.7726 kPa=<strong>0.6077 bar</strong>`

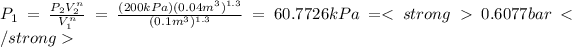
First:

`PV^n =constant\\P=constant V^(-n)`

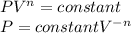
The work:

`W=\int\limits^2_1 {P} \, dV=\int\limits^2_1 {constant V^(-n)} \, dV\\W=(constant)((V^(-n+1))/(-n+1) )\left \{ {{2} \atop {1}} \right. \\W=(constant)((V_(2)^(-n+1)-V_(1)^(-n+1))/(-n+1) )\\W=(PV^n)((V_(2)^(-n+1)-V_(1)^(-n+1))/(-n+1) )\\W=((P_2V_2-P_1V_1))/(1-n)`

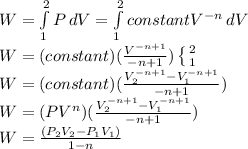
Substituting:

`W=((P_2V_2-P_1V_1))/(1-n)=((200kPa)(0.04m^3)-(60.7726kPa)(0.1m^3))/(1-1.3)`

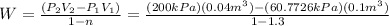
W=-6.4091 kJ