Question

A university claims that the mean time professors are in their offices for students is at least 6.5 hours each week. A random sample of eight professors finds that the mean time in their offices is 6.2 hours each week. With a sample standard deviation of 0.49 hours from a normally distributed data set, can the university’s claim be supported at α=0.05?

Answer 1

Answer with explanation:

Let
`\mu` be the population mean.

Null hypothesis :
`H_0: \mu\geq 6.5`

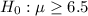
Alternative hypothesis :
`H_a: \mu<6.5`

Since alternative hypothesis is left-tailed , so the test is a left-tailed test.

Since n= 8 <30 , so we use t-test.

Test statistic for population mean :
`t=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}`

`t=(6.2-6.5)/((0.49)/(√(8)))\approx-1.73`

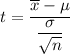
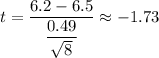
Critical value for t=
`t_(n-1, \alpha)=t_(7,0.05)=1.895`

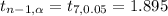
Since the absolute t-value (1.73) is less than the critical t-value(1.895), it means we are fail to reject the null hypothesis.

Thus , we conclude that we have enough evidence to support the university’s claim.