Question

Suppose that you are a student worker in the statistics department and they agree to pay you using the random pay system. Each week, the Chair flips a coin. If it comes up heads, your pay for the week is $80 and if it comes up tails your pay for the week is $40. Your friend is working for the engineering department and makes $65 per week. The probability that your total earnings in 100 weeks are more than hers is approximately...?

Answer 1

The probability of getting paid more than $6500 in 100 weeks is 0.6%

Step-by-step explanation:

In this problem, we need to define a probabilty distribution for the money earned.

The 100-week payoff can be expressed as

`PO=40*L+80*H=40*(100-H)+80*H=4000+40H`

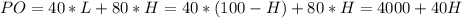
Being L the numbers of weeks we have low pay and H the weeks we have high pay.

Now, as it is a coin flip, H is a binomial random variable with p=0.5 and n=100

For a total pay off of more than 6500, H has to be

`6500=4000+40H\\\\H=2500/40=62.5`

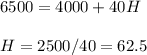
That means that in at least 63 of the 100 weeks we have to get a high pay.

`P(H\geq 63)=1-\sum_(i=1)^(62) P(X_i)`

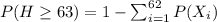
If we compute the individual probabilities we get P(H≥63)=0.006 or 0.6%.