Question

Find the percent by mass of tin in the original sample, assuming that it contains no other reducing agents. A sample of impure tin of mass 0.528 g is dissolved in strong acid to give a solution of Sn2+. The solution is then titrated with a 0.0448 M solution of NO3−, which is reduced to NO(g). The equivalence point is reached upon the addition of 4.03×10−2 L of the NO3− solution.

Answer 1

Step-by-step explanation:

The balanced equation for the given reaction is as follows.

`2NO^(-)_(3)(aq) + 3Sn^(2+)(aq) + 8H^(+) \rightarrow 2NO(g) + 3Sn^(4+) + 4H_(2)O`

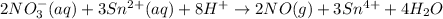
Number of moles of
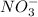`NO^(-)_(3)` consumed will be calculated as follows.

No. of moles =
`Molarity * {\text{volume in L}}`

=
`0.0448 M * 4.03 * 10^(-2) L`

=
`0.181 * 10^(-2) mol`

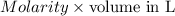
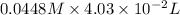
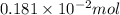
From the balanced equation, we get to know that 2 moles of
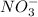`NO^(-)_(3)` reacts with 3 moles of
`Sn^(2+)` .

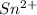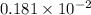`0.181 * 10^(-2)` moles of
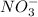`NO^(-)_(3)` reacts with M moles of
`Sn^(2+)`.

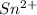M =
`(0.181 * 10^(-2)mol)/(2)`

=
`0.09 * 10^(-2) mol`

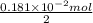
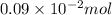
It is known that molar mass of tin is 118.71 g/mol. Hence, mass of Sn reacted will be as follows.

m =
`0.09 * 10^(-2)mol * 118.71 g/mol`

=
`10.68 * 10^(-2) g`

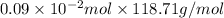
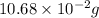
So, percent mass of tin in the original sample =
`\frac{\text{mass of tin reacted}}{\text{mass of sample}} * 100`

=
`(10.68 * 10^(-2) g)/(0.528 g) * 100`

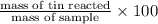
= 20.23 %

Thus, we can conclude that mass of tin is 20.23 %.