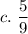Question

Find the probability of randomly rolling 2 standard dice and having a sum that is EVEN or GREATER THAN 9.

a.4/9
b.1/6
c.5/9
d.2/3

Answer 1

The answer is 5/9. Just took the quiz. Hope this helps. :)

Explanation:

Answer 2

Answer:
`c.\ (5)/(9)`

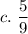
Explanation:

The total number of outcomes of rolling a die =6

Then , the total number of outcomes of rolling two dice = 6 x 6 = 36

Now , Pairs of outcomes having a sum that is EVEN = (1,1), (2,2), (3,3) , (4,4), (5,5), (6,6) , (1,3), (1,5), (2,4), (2,6), (3,1), (3,5), (4,2), (2,6),(5,3), (5,1), (6,4), (6,2)

i.e. Number of outcomes having a sum that is EVEN = 18

Pairs of outcomes having a sum that is GREATER THAN 9 = (4,6), (6,4), (5,5), (5,6), (6,5), (6,6)

i.e. Number of outcomes having a sum that is GREATER THAN 9 =6

Number of outcomes having a sum that is EVEN and GREATER THAN 9 ((4,6), (6,4), (5,5), (6,6)) = 4

Now , the Number of outcomes having a sum that is EVEN or GREATER THAN 9 = (Number of outcomes having EVEN sum)+(Number of outcomes having sum GREATER THAN 9 )-(Number of outcomes having a sum EVEN and GREATER THAN 9 )

= 18+6-4=20

Now , the probability of randomly rolling 2 standard dice and having a sum that is EVEN or GREATER THAN 9 =
`\frac{\text{Number of rollings having a sum that is EVEN or GREATER THAN 9 }}{\text{Total outcomes}}\\\\=(20)/(36)=(5)/(9)`

Hence, the correct answer is
`c.\ (5)/(9)`