Question

X≥1 x≤7 y≥-1/3x+6

Which graph best represents the feasibility region for the system shown above?

Answer 1

Explanation:

i am unsure of what you actually need, but i want to help you.

if you were to set the boundaries of the feasibility region it would be as follows:

as points

A(1, 17/3) B(7, 11/3) C(7, infinity) D(1, infinity)

as graphs

y=-1/3x+6 where 1≤x≤7

x=1

x=7

Answer 2

The feasible region for the system is shown below.

Explanation:

The given system of inequality is shown below,

`x\geq 1`

`x\leq 7`

`y\geq -(1)/(3)x+6`

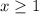
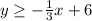
The related equation of first two inequalities are x=1 and x=7 respectively. Both are vertical lines solid lines because the points on the lines are included in the solution set.

The first inequality is
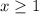`x\geq 1`, so shade the area to the right.

The second inequality is
`x\leq 7`, so shade the area to the left.

The related equation of third inequality is

`y=-(1)/(3)x+6`

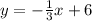
Here, the slope of the line is -1/3 and y-intercept is 6.

At x=3,

`y=-(1)/(3)(3)+6=5`

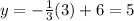
Plot these two points (0,6) and (3,5) on the coordinate plane and connect them by a straight line.

Check the inequality by (0,0).

`0\geq -(1)/(3)(0)+6`

`0\geq 6`

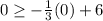
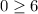
This statements is false. It means (0,0) is not included in the shaded region of third inequality.

So, shade the area above the related line and related line is a solid line because the sign of inequality is ≥.

Therefore, the common shaded region represents the feasibility region.