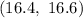Question

The electric cooperative needs to know the mean household usage of electricity by its non-commercial customers in kWh per day. Assume that the population standard deviation is 2.5 kWh. The mean electricity usage per family was found to be 16.5 kWh per day for a sample of 3861 families. Construct the 98% confidence interval for the mean usage of electricity. Round your answers to one decimal place.

Answer 1

Answer:
`(16.4,\ 16.6)`

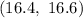
Explanation:

Given : Sample size : n= 3861

Significance level :
`\alpha=1-0.98=0.02`

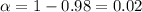
Critical value for significance level of
`\alpha=0.02` :
`z_(\alpha/2)= 2.33`

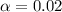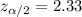
Sample mean :
`\overline{x}=16.5`

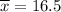
Standard deviation :
`\sigma= 2.5`

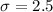
The formula to find the confidence interval for population mean is given by :-

`\overline{x}\pm z_(\alpha/2)(\sigma)/(√(n))`

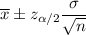
i.e
`16.5\pm (2.33)(2.5)/(√(3861))`

`=16.5\pm0.0937445500445\\\\\approx16.5\pm0.1=(16.5-0.1,\ 16.5+0.1)=(16.4,\ 16.6)`

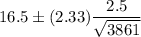
Hence, the 98% confidence interval for the mean usage of electricity :

`(16.4,\ 16.6)`