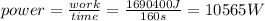Question

A car of mass 1600 kg traveling at 27.0 m/s is at the foot of a hill that rises vertically 135 m after travelling a distance of 3.20 km. At the top of the hill, the speed of the car is 14.0 m/s. Find the average power delivered by the car's engine, neglecting any frictional losses.

Answer 1

Neglecting any frictional losses, the average power delivered by the car's engine is 10565 W

Step-by-step explanation:

The energy conservation law indicates that the energy must be the same at the bottom of the hill and at the top of the hill.

The energy at the bottom is only the Kinect energy (K_1) of the car in motion, but in the top, the energy is the sum of its Kinect energy (K_2), potential energy (P) and the work (W) done by the engine.

`K_1 = K_2 + P + W`

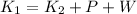
then, the work done by the engine is:

`W = K_1 - K_2 - P`

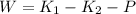
The formulas for the Kinetic and potential energy are:

`K=(1)/(2)mV^2\\P=mgh`

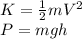
where, m is the mass of the car, V the velocity, g the gravity and h is the elevation of the hill.

Using the formulas:

`W=(1)/(2)mV_1^2-(1)/(2)mV_2^2-mgh`

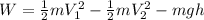
Replacing the values:

`W=(1)/(2)(1600Kg)(27m/s)^2-(1)/(2)(1600Kg)(14m/s)^2-(1600Kg)(9.8m/s^2)(135m)\\W=-1690400 J`

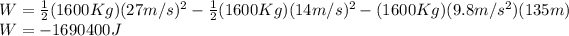
The negative of this value indicates the direction of the work done, but for the problem, you only care about the magnitude, so the power is W=1690400 J. Now, the power is equal to work/time so you need to find the time the car took to get to the top of the hill.

The average speed of the car is (27+14)/2=20m/s, and t=d/v so the time is:

`t=(3200m)/(20m/s)=160s`

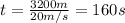
the power delivered by the car's engine was:

`power=(work)/(time)=(1690400J)/(160s)=10565W`