Answer:
The expected net profit of the company is $400.
Explanation:
In this problem we work with the Expected Value, which represents the representative average value according to the probabilities of the different events and their effect on the result. In this case is the Expected net profit.
The equation for the Expected Value is:
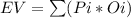
being Pi: the probability of Event i and Oi: the impact or outcome of event i.
In this case:
Event 1 is the $5000 claim. The probability of this event is 20% and the outcome is -$5000+$4000 = -$1000.
Event 2 is the $1000 claim. The probability of this event is 60% and the outcome is -$1000+$4000 = +$3000.
Event 3 is the $20000 claim. The probability of this event is 10% and the outcome is -$20000+$4000 = -$16000.
Event 4, is the no-claim event. The probability of this event is 10% and the outcome is -$0+$4000 = +$4000.
All four events sum a probability of 100%.
We can calculate the Expected net profit as:
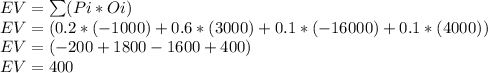
The expected net profit of the company is $400.