Answer with explanation:
Null hypothesis :
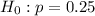
Alternative hypothesis :
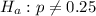
Given : A genetic experiment with peas resulted in one sample of offspring that consisted of 429 green peas and 159 yellow peas.
i.e.
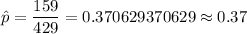
For 95% level of confidence, significance level :
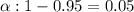
Critical value of z =
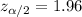
Confidence interval for population proportion :
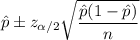

Since 0.25 is not contained in the confidence interval , it means is not reasonable that the true proportion is 0.25 (25%).
Thus, the results contradicts the expectations.