Question

A genetic experiment with peas resulted in one sample of offspring that consisted of 429 green peas and 159 yellow peas. a. Construct a 95​% confidence interval to estimate of the percentage of yellow peas. b. It was expected that​ 25% of the offspring peas would be yellow. Given that the percentage of offspring yellow peas is not​ 25%, do the results contradict​ expectations? a. Construct a 95​% confidence interval. Express the percentages in decimal form.

Answer 1

Answer with explanation:

Null hypothesis :
`H_0:p=0.25`

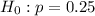
Alternative hypothesis :
`H_a:p\\eq0.25`

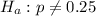
Given : A genetic experiment with peas resulted in one sample of offspring that consisted of 429 green peas and 159 yellow peas.

i.e.
`\hat{p}=(159)/(429)=0.370629370629\approx0.37`

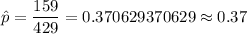
For 95% level of confidence, significance level :
`\alpha:1-0.95=0.05`

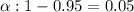
Critical value of z =
`z_(\alpha/2)=1.96`

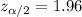
Confidence interval for population proportion :

`\hat{p}\pm z_(\alpha/2)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`=0.37\pm(1.96)\sqrt{(0.37(1-0.37))/(429)}\\\\=0.37\pm0.0456876228438\\\\\approx0.37\pm0.05\\\\=(0.37-0.05,0.37+0.05)=(0.32,0.42)`

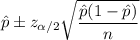
Since 0.25 is not contained in the confidence interval , it means is not reasonable that the true proportion is 0.25 (25%).

Thus, the results contradicts the expectations.